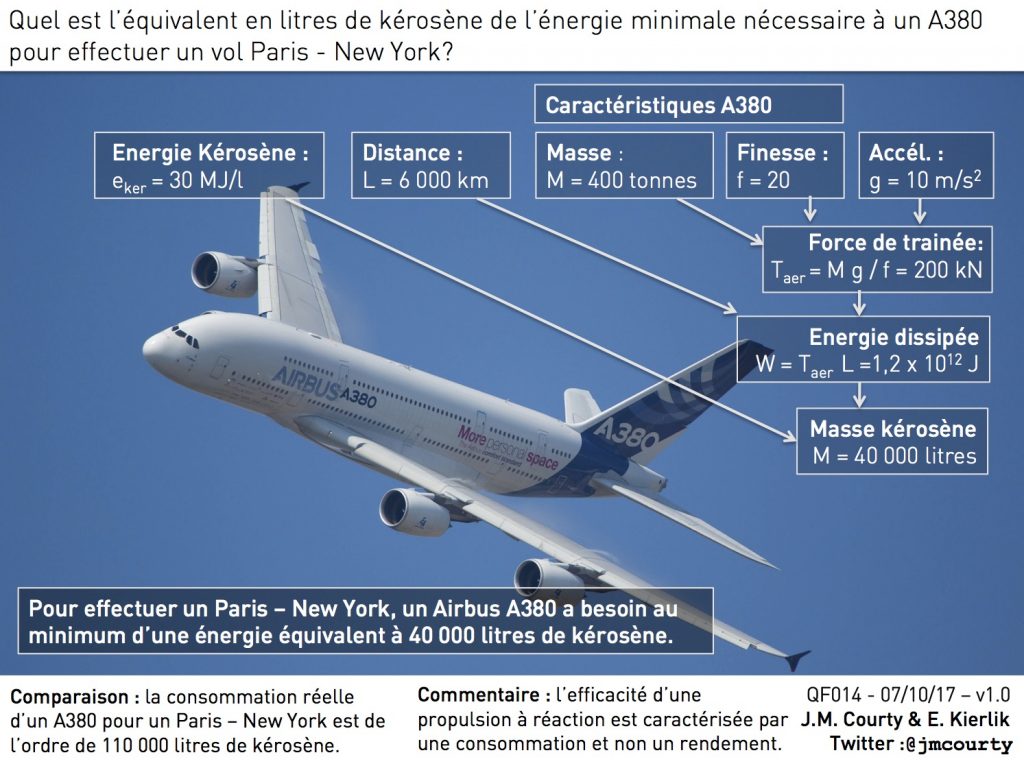
Pour effectuer un vol Paris – New York, un Airbus A380 a besoin au minimum d’une énergie équivalent à 40 000 litres de kérosène.
Le principe de la résolution
Tout d’abord, nous centrons cette question sur l’énergie nécessaire pour le vol de l’avion. Nous ne considérerons pas tout ce qui concerne le fonctionnement des équipements. Il s’agit donc de faire un bilan énergétique mécanique. L’avion est soumis à deux forces : son poids et la force exercée par l’air. Cette force aérodynamique peut être décomposée en deux : la trainée \( T_\rm{aero} \), parallèle à la vitesse de l’avion et opposée à celle ci, et la portance \( P_\rm{aero}\), perpendiculaire à la vitesse de l’avion (donc pour laquelle le travail est nul). Le travail fourni par le poids lors de la montée est stocké en énergie potentielle et récupéré lors de la descente, il n’est donc pas nécessaire de le considérer. Ne reste donc que le travail de la force de trainée.
Il s’agit donc en définitive d’évaluer le travail de la force de trainée sur tout le parcours en supposant que celui ci a lieu horizontalement et à vitesse constante.
Le résultat crucial qui permet d’obtenir cette force de trainée est le suivant : le rapport \( \frac{P_\rm{aero}}{T_\rm{aero}} \) entre la force de portance et la force de trainée ne dépend pas de la vitesse. Il est égal au rapport \( \frac{C_\rm{z}}{C_\rm{x}} \) entre le coefficient de portance et le coefficient de trainée, qui n’est autre que la finesse \( f \) de l’avion. Pour plus de détails sur la finesse , voir l’article wikipedia.
Le raisonnement est alors le suivant :
- la vitesse est constante donc la somme des forces est nulle.
- la projection sur un axe vertical nous apprend que la force de portance est égale au poids \( P_\rm{aero} = M \, g \)
- La trainée est égale au rapport de cette force et de la finesse \( T_\rm{aero} = \frac{P_\rm{aero}}{f} = \frac{M \, g}{f} \)
- Le travail \( W_T \) de la trainée est le produit de cette force par la distance \( L \) parcourue soit \( W_T = \, – T_\rm{aero} \, L =\, – \frac{M \, g \, L}{f} \)
- L’énergie minimale nécessaire pour le vol est l’opposée de ce travail : \( W_{\min} = \, -W_T = \frac{M \, g \, L}{f} \)
Les chiffres
Nous avons besoin de la masse d’un A380, de sa finesse, de la distance Paris New York et du contenu énergétique d’un litre de kérosène.
Nous disposons des valeurs suivantes (source : wikipédia):
- Masse maximum à vide : 369 tonnes
- Masse à vide : 276,8 tonnes
- Masse maximum au décollage : 575 tonnes
- Masse maximum à l’atterrissage : 394 tonnes.
Nous prendrons comme valeur la moyenne des extrêmes soit une masse égale à 400 tonnes.
La finesse de l’A380 est de 20 (source : wikipedia)
La distance Paris New-York est de 5840 kilomètres. Nous prendrons comme valeur de la distance, 6000 kilomètres.
Le contenu énergétique du kérosène est de 43 mégajoules par kilogramme soit 33 mégajoules par litre.
Discussion du résultat
Ces valeurs donnent une consommation énergétique minimale de 40 000 litres
Nous pouvons comparer cette valeur à la consommation d’un A380 est de 106 000 litres soit 85 tonnes.